Architecture

The first step performed during the design phase was to identify the different software components that would conform the final project. The components identified during the design phase, along with their depencies, are illustrated below. Components referring to command line tools are highlighted in yellow.

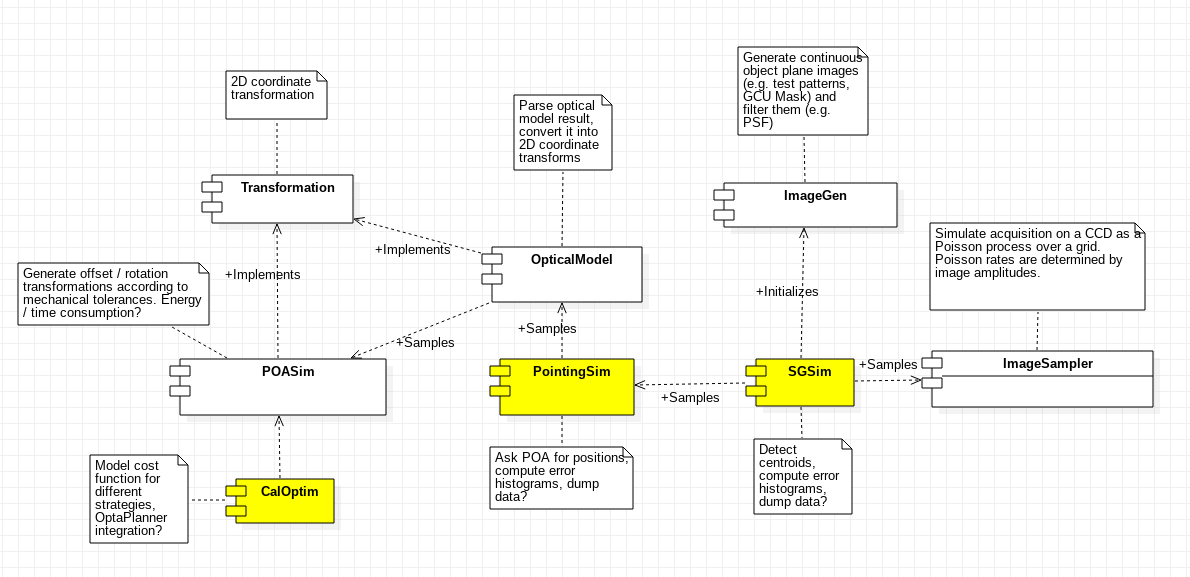
Common

The common component represents the set of generic utility classes used across the project, like float array, exceptions and quantities.

class FloatArray(shape, buffer=None, offset=0, strides=None, order=None)

Convenience subclass of numpy.ndarray with helper methods that ensures all arrays created from miscellaneous Python objects like tuples or lists are of the same ARRAY_TYPE type. Currently, ARRAY_TYPE is defined as float32, giving a 24-bit significand (slightly more than 7 decimals of precission). This class also provides a unified way to define tensors in harmoni-pm

Constructor parameters are that of the underlying numpy.ndarray constructor with dtype set to ARRAY_TYPE.

static make(lst)

Factory method that instantiates a FloatArray from a given Python list or tuple specified by lst. This lst is passed directly to the underlying numpy.ndarray constructor, and therefore the usual list/tuple - numpy.ndarray conversion rules apply.

static compatible_with(arr)

Returns True if arr is derived from numpy.ndarray and its dtype is set to ARRAY_TYPE. Otherwise, return false.

class Configuration

class InvalidPrototypeError

class InvalidTensorShapeError

class QuantityType

Transformation

The Transformation component provides the abstraction to handle coordinate transforms between conjugate planes, assuming Gaussian optics (i.e. diffractive effects are ignored and must be modeled separately). Under this approximation, transforms are just \(\mathbb R^2\to\mathbb R^2\) functions between coordinates.

Something as simple as a telescope with a given focal length can be modeled as a coordinate transform that multiplies the input coordinates by the inverse of the focal length. The following clases belong to the Transformation component:

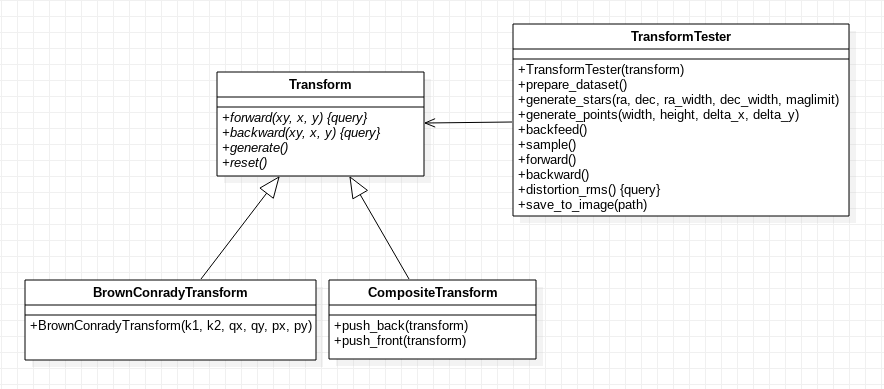
class Transform

This is the abstract class from which all other coordinate transforms are derived. If instatiated directly, it represents the identity transform. Transforms accept tuples of the form \((x, y)\) or \(N\times2\) FloatArray arrays representing sets of \(N\) coordinates.

_forward(xy)

Protected method that computes the forward transform over the ARRAY_TYPE tuple xy and returns a \(1\times2\) FloatArray containing the transformed coordinates. Non-trivial derivations of Transform must override at least _forward and _backward.

_backward(xy)

Protected method that computes the backward transform over the ARRAY_TYPE tuple xy and returns a \(1\times2\) FloatArray containing the transformed coordinates. Non-trivial derivations of Transform must override at least _forward and _backward.

_forward_matrix(matrix)

Protected method that performs \(N\) forward coordinate transforms all at once over the coordinate list matrix in the form of a \(N\times2\) FloatArray and returns the transformed coordinate list as another \(N\times2\) FloatArray. If not overriden by the subclass, this method simply applies _forward along the \(N\) rows of matrix.

_backward_matrix(matrix)

Protected method that performs \(N\) backward coordinate transforms all at once over the coordinate list matrix in the form of a \(N\times2\) FloatArray and returns the transformed coordinate list as another \(N\times2\) FloatArray. If not overriden by the subclass, this method simply applies _backward along the \(N\) rows of matrix.

forward(xy=None, x=None, y=None)

Public method that performs a forward transform, accepting either two scalar coordinates x and y or a tuple / FloarArray of coordinates in xy. The method automatically determines whether to use _forward of _forward_matrix according to the arguments passed to it.

backward(xy=None, x=None, y=None)

Public method that performs a forward transform, accepting either two scalar coordinates x and y or a tuple / FloarArray of coordinates in xy. The method automatically determines whether to use _backward of _backward_matrix according to the arguments passed to it.

generate()

In case the transform is derived from a set of parameters with uncertainties (e.g. mechanical tolerances, misalignments, precission limits in measurements), this method is called during Monte Carlo testing to initialize the specific transform parameters by drawing a sample from each parameter distribution.

reset()

In case the transform holds a state (e.g. energy consumed during operation, time variation of the parameter distributions, etc), this method sets any internal state variables to their initial values.

class CompositeTransform

The CompositeTransform represents a chain of transforms \(T_{1},T_{2}, ... ,T_{n}\) that are applied sequentially according to the transform direction. If \(T_1\) represents the coordinate transform between the object plane and the rest of the chain and \(T_n\) the transform between the rest of the chain and the object plane, the forward composite transform is simply \(T_{cf}=T_{nf}\circ \dots \circ T_{2f}\circ T_{1f}\). The backward transform will be \(T_{cb}=T_{cf}^{-1}=(T_{nf}\circ \dots \circ T_{2f}\circ T_{1f})^{-1}=T_{1f}^{-1}\circ T_{2f}^{-1}\circ \dots \circ T_{nf}^{-1}=T_{1b}\circ T_{2b}\circ \dots \circ T_{nb}\).

push_front(T)

Puts the transform T in the frontmost position of the transform chain, becoming the first transform to be computed in the forward direction.

push_front(T)

Puts the transform T in the backmost position of the transform chain, becoming the first transform to be computed in the backward direction.

class TransformTester(T)

As new transforms are expected to be implemented in the future, a tester class TransformTester with transform debugging functions is provided. TransformTester is instantiated from a given transform \(T\) and can generate a set of coordinates (the so-called departure coordinates), either from a regular grid or from a set of stars in the sky up to certain visual magnitude. Then, a copy of these coordinates (the current coordinates) can be transformed multiple times in both directions by applying \(T\) by means of the tester API. Finally, the tester API also allows the user to measure how much the current coordinates deviate from the departure coordinates and produce image files representing these deviations.

Images produced by TransformTester using a regular grid of points (left) and stars in the sky (right).

generate_stars(ra, dec, ra_width, dec_width, maglimit)

Initializes the departure coordinates from a set of stars in the sky enclosed in a rectangle centered in right ascension ra and declination dec, and dimensions ra_width x dec_width (both of them in degrees) up to magnitude maglimit. Right ascension is encoded in the \(x\) coordinate and declination in the \(y\) coordinate.

generate_points(width, height, delta_x, delta_y)

Initializes the departure coordinates from a set of equally spaced points, assuming a rectangle of size width x height with a delta_x separation in the horizontal dimension and delta_y separation in the vertical dimension.

forward()

Applies the transform T to the current coordinates in the forward direction and replaces them by the result of the transform

backward()

Applies the transform T to the current coordinates in the forward direction and replaces them by the result of the transform.

backfeed()

Replaces the departure coordinates by the current coordinates, effectively behaving as if the tester departure points were generated from the current state.

sample()

Call T.generate() in order to sample the parameter distribution of the transform.

distortion_rms()

Returns the root-mean-square value of the difference between the current coordinates and the departure coordinates. This value is computed as:

\[E = \left[\frac{1}{N}\sum_{i=1}^N (x_i-\tilde{x}_i)^2+(y_i-\tilde{y}_i)^2\right]^{1/2}\]

With \((x_i, y_i)\) the departure coordinates and \((\tilde{x}_i,\tilde{y}_i)\) the current (potentially transformed) coordinates.

save_to_image(path)

Produce an image describing the result of the transformation with respect to the departure points, along with technical information like the exact sequence of applied transformations and the transform RMS.

ImageGen

The ImageGen component provides an abstraction for images both in the sky and the focal plane called Image Planes indistinctively. In this context, an Image Plane is simply a radiative intensity field \(I(\vec{q}): \mathbb R^2\to\mathbb R\), where \(\vec{q}=(\alpha,\delta)\) if the field describes objects in the sky, or \(\vec{q}=(x,y)\) if the field refers to the intensity in the focal plane.

Image planes are transformed by the optical model and sampled by ImageSampler, which takes into account focal distances, obstructions, entrance pupils, etc. and determines not only how much light arrives to the focal plane, but also how sky coordinates are translated into focal plane coordinates and the intensity is converted into flux.

The intensity returned by image planes, as well as of the rest of magnitudes handled internally by harmoni-pm, has SI units (\(\text{J m}^{-2}\text{sr}^{-1}\text{s}^{-1}\text{Hz}^{-1}\)).

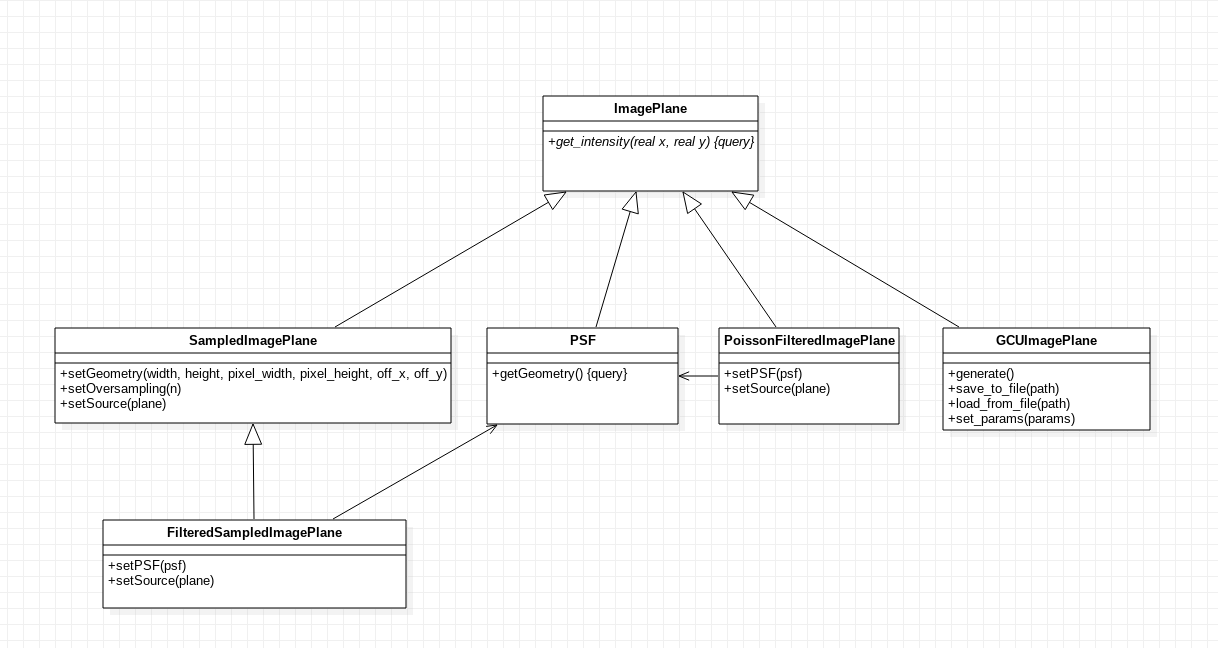
class ImagePlane

Base class for all implementations of image planes.

class GCUImagePlane(params=None)

Specialization of ImagePlane that attempts to reproduce the intensity map of a regular grid of homogeneously-illuminated circles, mimicking the GCU mask of the instrument. If specified, params is a dictionary whose keys describe parameters to be adjusted. Unrecognized parameters are ignored. Accepted parameters are:

• point.separation: separation of the circle centers in both dimensions (\(\text{m}\)). Default: \(15\times10^{-3}\)

• point.diameter: diameter of each circle (\(\text{m}\)). Default: \(150\times10^{-6}\)

• point.intensity: intensity of each circle (\(\text{J m}^{-2}\text{sr}^{-1}\text{s}^{-1}\text{Hz}^{-1}\)). Default: \(10^{-3}\)

• point.x0: horizontal displacement of the mask (\(\text{m}\)). Default: \(0\)

• point.y0: vertical displacement of the mask (\(\text{m}\)). Default: \(0\)

• mask.diameter: diameter of the mask (\(\text{m}\)). Default: \(0.4\)

generate()

Initialize the GCU by drawing random samples from its parameter distributions.

save_to_file(path)

Save parameters to a file.

load_from_file(path)

Retrieve parameters from a file.

set_params(params)

Updates the GCU parameters according to the dictionary specified in params (see constructor for details).

OpticalModel

The optical model is responsible for integrating known information about the instrument that may affect the behavior of the optics between the entrance pupil and the CCD. This information may include mechanical tolerances, optical aberrations, thermal effects, etc. along with their corresponding uncertaintites. As a result, the optical model produces a coordinate transformation between the entrance pupil and the exit pupil.

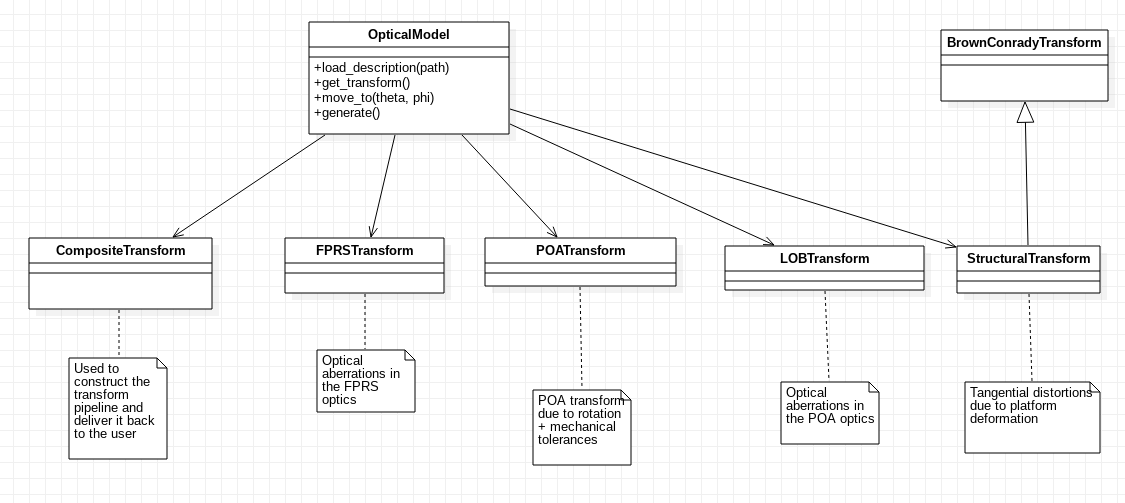
ImageSampler

The ImageSampler component attempts to reproduce the image acquired by a CCD assuming an intensity field given by an ImagePlane object is placed in the entrance pupil of the optical model described by an OpticalModel object, simulating the image produced by the instrument. The ImageSampler is also in charge of translating the input intensity map into a flux map that can be used to integrate the image in the CCD.

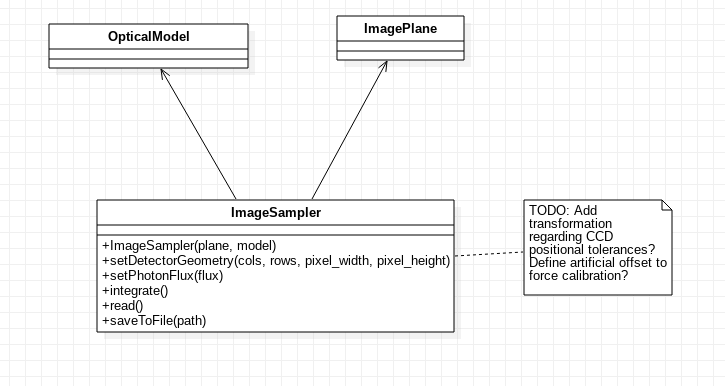
class ImageSampler(plane, model)

Initializes the ImageSampler main object, from a given sky/mask ImagePlane as first argument and OpticalModel as second argument. The ImageSampler is set with a default oversampling value of HARMONI_IMAGE_SAMPLER_OVERSAMPLIGN (currently 8). Parallelization is set to true by default.

set_oversampling(oversampling)

Sets the oversampling value to oversampling. This operation triggers the precalculation of all intermediate data like the coordinate offset matrices and the CCD matrix.

set_geometry(cols, rows, delta_x, delta_y, finv=1)

Sets the geometry of the CCD to cols columns wide, rows rows tall, and with pixel sizes delta_x x delta_y, both in meters. The optional argument finv establishes adjusts the plate scale between the last optical element in the OpticalModel optics and the CCD.

set_parallel(val)

Enables or disables parallelization according to the boolean value val.

integrate()

Triggers integration of the sky intensity function passed to the constructor, in a serial or parallel fashion according to the current parallelization configuration. Returns a tuple with the following information, in order:

1. Number of slices of the CCD.

2. The mean computation time of each integration slice.

3. The standard deviation of the computation time of all slices.

4. Total integration time (in seconds).

TODO: specify integration time!

integrate_serial():

Force computation of all slices in one thread (equivalent to calling integrate() with parallelization disabled). No value is returned.

integrate_parallel():

Force computation of all slices in one thread (equivalent to calling integrate() with parallelization enabled). No value is returned.

save_to_file(path):

Saves the image produced by the CCD to an image file specified by path.